Leyland number

A Leyland number is a number that can be expressed in the form [math]\displaystyle{ x^y+y^x }[/math], where x and y are positive integers with the condition 1 < x ≤ y. These numbers are named after Paul Leyland, who first studied these numbers in 1994. The first few nontrivial Leyland numbers are given by OEIS sequence A076980.

A Leyland prime is a Leyland number which is also a prime (see sequence A094133 in OEIS).

The second kind of numbers are of the form [math]\displaystyle{ x^y-y^x }[/math].

Data

The data tables contains for every number the x and y values, the number of digits, the Leyland number, dates and persons of finding and proving if available and the program used to prove a prime.

Leyland numbers

There are 1,814 numbers: 307 proven primes and 1,507 probable primes.

• Category
• Table

Leyland numbers second kind

• Category

Reservation history

x=20001-40000, y=11-200 completed by Serge Batalov, 2014-05-03

x=15001-20000, y=1001-2000 completed by Serge Batalov, 2014-05-14

x=40001-330000, y=11-17 completed by Serge Batalov, 2014-05-16

x=330001-400000, y=11-17 completed by Serge Batalov, 2014-05-17

x=400001-500000, y=11-17 completed by Serge Batalov, 2014-05-19

x=20001-30000, y=801-1000 reserved by Dylan Delgado, 2019-07-24

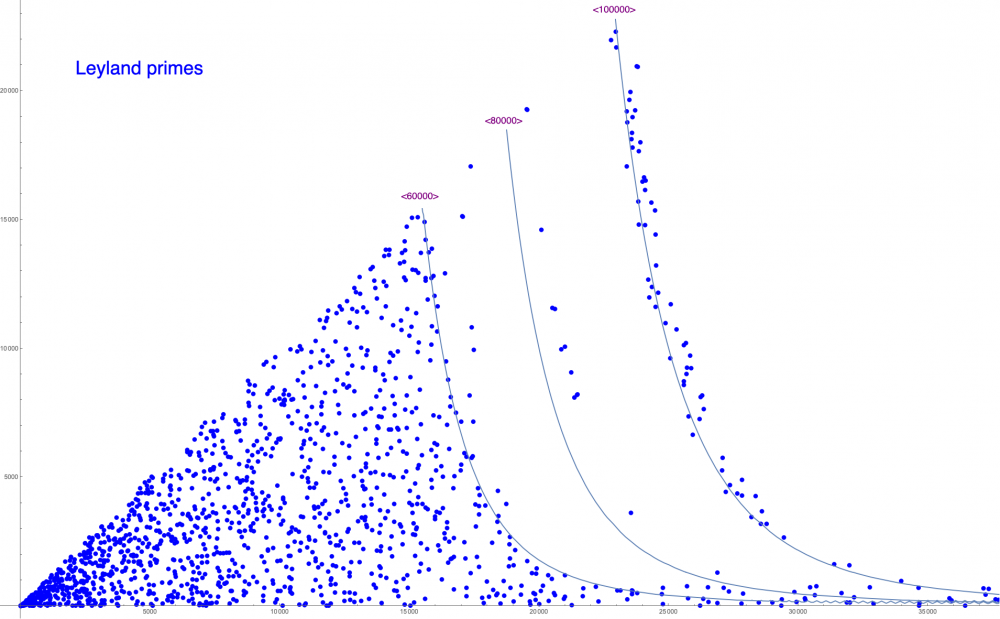
Contribution of Leyland numbers

This graph can be found here:

External links

• Leyland number
• Main thread of XYYXF Project at MersenneForum
• Current search for Leyland PRP's at MersenneForum
• Prime proofs of Leyland numbers at MersenneForum
• Homepage of Paul Leyland
• Page of Leyland numbers, dated 2006-10-06 by P.Leyland
• Homepage of Andrey Kulsha, dated 2017-01-04
• Yahoo group, 2005 to 2016
• sequence A061119 in OEIS of n^2 + 2^n
• sequence A253471 in OEIS of n^3 + 3^n
• YouTube "Leyland Numbers - Numberphile"

Number classes

General numbers

Integer Natural Even Odd Rational Irrational Real Prime Probable prime

Special numbers

Mersenne 2n-1 Fermat 22n+1 Proth k•2n+1 Riesel k•2n-1 Woodall n•2n-1 Cullen n•2n+1 Double Mersenne 22p-1-1 Perfect 2n-1(2n-1) Leyland xy ± yx Gen.Repunit (b^n-1)/(b-1)

Prime numbers

Mersenne Proth Riesel Williams (b±1)bn±1 Carol/Kynea (bn±1)2-2 Multifactorial n!j±1