| Currently there may be errors shown on top of a page, because of a missing Wiki update (PHP version and extension DPL3). |
Navigation
| Topics | Help • Register • News • History • How to • Sequences statistics • Template prototypes |
Leyland number
A Leyland number is a number that can be expressed in the form [math]\displaystyle{ x^y+y^x }[/math], where x and y are positive integers greater 1 and x ≥ y. These numbers are named after Paul Leyland, who first studied these numbers in 1994. The first few nontrivial Leyland numbers are given by OEIS sequence A076980.
A Leyland prime is a Leyland number which is also a prime (see sequence A094133 in OEIS).
The second kind of numbers are of the form [math]\displaystyle{ x^y-y^x }[/math].
Contents
History
Data
The data tables contains for every number the x and y values, the number of digits, the Leyland number[1], dates and persons of finding and proving if available and the program used to prove a prime.
Leyland numbers
There are 1,814 numbers: 307 proven primes and 1,507 probable primes.
Leyland numbers second kind
Reservation history
First kind (plus form)
| Range x | Range y | Digits | Reserved by | Reserved | Completed | Found |
|---|---|---|---|---|---|---|
| 3 - 1030 | ~ 2 - 3000 | Paul Leyland | 1994 | 1997 | 88 | |
| 1031 - 1050 | ~ 700 - 2800 | Paul Leyland | 2001-06-04 | 2001-06-04 | 4 | |
| 1051 - 1500 | ~ 2000 - 4600 | Andrey Kulsha | 2001-06-03 | 2001-06-23 | 41 | |
| 1501 - 1700 | ~ 2600 - 5100 | Paul Leyland | 2001-06-05 | 2001-06-11 | 18 | |
| 1701 - 2000 | Christ van Willegen | 2001-06-05 | 2001-06-09 | 23 | ||
| 2001 - 2200 | Greg Childers | 2001-06-07 | 2001-06-09 | 19 | ||
| 2201 - 2400 | Greg Childers | 2001-06-09 | 2001-06-12 | 17 | ||
| 2401 - 2600 | Peter Liaskovsky | 2001-08-31 | 2001-09-03 | 22 | ||
| 2601 - 2700 | Paul Leyland | 2001-07-24 | 2001-08-08 | 13 | ||
| 2701 - 2800 | Greg Childers | 2001-07-30 | 2001-07-31 | 7 | ||
| 2801 - 3000 | Greg Childers | 2001-07-31 | 2001-08-05 | 14 | ||
| 3001 - 3050 | Sander Hoogendoorn | 2001-06-14 | 2001-06-19 | 2 | ||
| 3051 - 3100 | Peter Liaskovsky | 2001-09-03 | 2001-09-05 | 6 | ||
| 3101 - 3200 | Alexander Kuzmich | 2001-09-16 | 2001-10-06 | 12 | ||
| 3201 - 3379 | Leonid Muraviov | 2001-11-28 | 2002-03-28 | 12 | ||
| 3380 - 3500 | Andrey Kulsha | 2002-04-19 | 2002-05-19 | 7 | ||
| 3501 - 4400 | Paul Leyland | 2001-12-21 | 2002-06-27 | 70 | ||
| 4401 - 4500 | Greg Childers | 2002-07-13 | 2002-08-13 | 9 | ||
| 4501 - 5000 | Mark Rodenkirch | 2002-09-07 | 2002-11-19 | 42 | ||
| 5001 - 5100 | Paul Leyland | 2003-06-13 | 2003-06-23 | 11 | ||
| 5101 - 5200 | Paul Leyland | 2003-06-23 | 2003-07-16 | 5 | ||
| 5201 - 5500 | Greg Childers | 2003-07-21 | 2003-09-17 | 17 | ||
| 5501 - 7500 | Anatoly Selevich | 2003-06-25 | 2004-08-07 | 154 | ||
| 20001 - 40000 | 11 - 200 | Serge Batalov | 2014-05-13 | 2014-05-14 | 17 | |
| 15001 - 20000 | 1001 - 2000 | Serge Batalov | 2014-05-14 | 2014-05-14 | 20 | |
| 40001 - 330000 | 11 - 17 | Serge Batalov | 2014-05-15 | 2014-05-16 | 3 | |
| 330001 - 400000 | 11 - 17 | Serge Batalov | 2014-05-16 | 2014-05-17 | - | |
| 400001 - 500000 | 11 - 17 | Serge Batalov | 2014-05-17 | 2014-05-19 | - | |
| 20001 - 40000 | 201 - 400 | Norbert Schneider | 2014-07-09 | 2015-08-10 | ||
| 12051 - 12500 | 2001 - x-1 | Norbert Schneider | ? | 2014-05-26 | 4 | |
| 2501 - 3000 | 12501 - 15000 | Vincent Gautier | 2014-11-04 | 2014-11-14 | 6 | |
| 300000 - 500000 | 18 | Andrey Kulsha | 2014-12-02 | |||
| 40001 - 50000 | 19 - 400 | Norbert Schneider | 2014-12-02 | 2015-10-23 | - | |
| 50001 - 500000 | 19 - 25 | Norbert Schneider | 2015-01-26 | |||
| 12501 - 13000 | 3001 - x-1 | Norbert Schneider | 2015-10-23 | 2016-04-21 | - | |
| 13000 - 15,000 | Norbert Schneider | 2019-03-27 | ||||
| 20001 - 50000 | 401 - 800 | Norbert Schneider | 2016-04-21 | |||
| 20001 - 30000 | 801 - 1000 | Dylan Delgado | 2019-07-24 |
Double checks
- 2014-07-27: Mark Rodenkirch checked x ≤ 12500, y ≤ 2500
- 2014-08-03: Mark Rodenkirch checked x ≤ 12500, y ≤ 5000
- 2014-07-27: Mark Rodenkirch checked x ≤ 12500, 10000 < y ≤ 12500
- 2014-08-07: Mark Rodenkirch checked x ≤ 12500, y ≤ 7000
- 2014-08-28: Mark Rodenkirch checked x ≤ 12500, y ≤ 12500
Second kind (minus form)
| Range x | Range y | Digits | Reserved by | Reserved | Completed | Found |
|---|---|---|---|---|---|---|
| 3 - 10200 | Norbert Schneider | 2010 | 2015-04-03 | 1553 | ||
| 10201 - 10400 | Norbert Schneider | 2015-04-05 | 2015-06-15 | 30 | ||
| 10401 - 10600 | Norbert Schneider | 2015-07-23 | 2015-10-21 | 33 | ||
| 10601 - 10800 | Norbert Schneider | 2015-10-29 | 2016-01-21 | 20 | ||
| 10801 - 11000 | Norbert Schneider | 2016-01-27 | 2016-06-04 | 24 | ||
| 11000 - 11300 | Norbert Schneider | 2016-02-19 | 2016-10-19 | 34 | ||
| 11300 - 12400 | Mark Rodenkirch | 2016-03-26 | 2016-07-22 | 118 | ||
| 12401 - 12500 | Norbert Schneider | 2012-08-29 | 2013-08-27 | 13 | ||
| 12501 - 13000 | Norbert Schneider | 2016-04-10 | 35 | |||
| 13001 - 15000 | 41 - 1200 | Norbert Schneider | ||||
| 15001 - 20000 | 41 - 100 | Dylan Delgado | 2019-08-04 | 2019-08-05 | 5 | |
| 30001 - 30100 | Norbert Schneider | 2014-08-12 | 4 | |||
| 70001 - 100000 | 11 - 20 | Dylan Delgado | 2019-08-05 | 2019-08-17 | 1 | |
| 70001 - 140000 | Norbert Schneider |
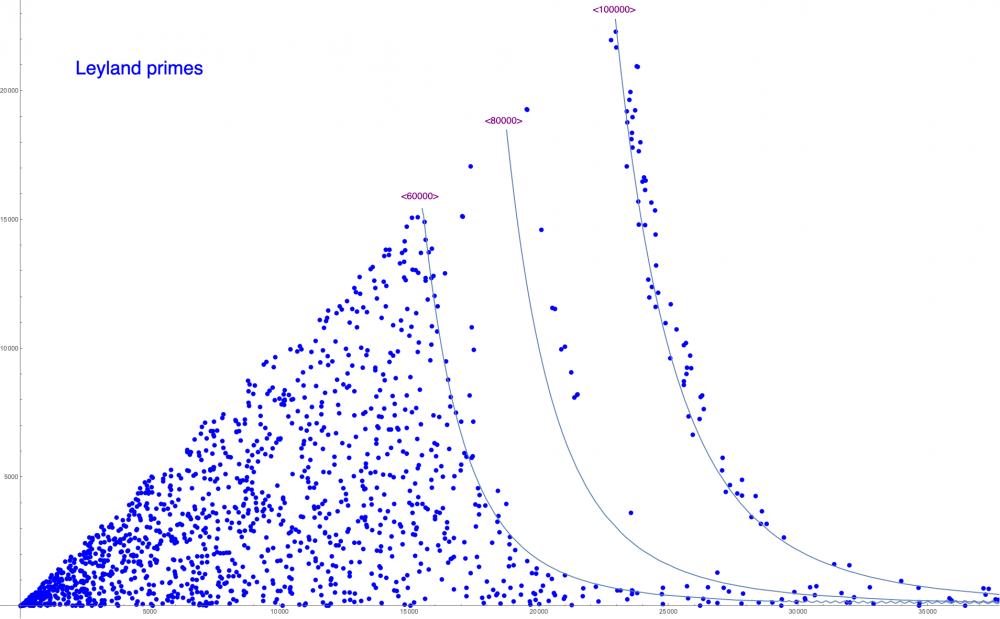
Contribution of Leyland numbers
This graph can be found here:
References
External links
- Leyland number
- Main thread of XYYXF Project at MersenneForum
- Current search for Leyland PRP's at MersenneForum
- Prime proofs of Leyland numbers at MersenneForum
- Search of x^y-y^x numbers at MersenneForum
- Search page of Norbert Schneider
- Homepage of Paul Leyland
- Page of Leyland numbers, dated 2006-10-06 by P.Leyland
- Homepage of Andrey Kulsha, dated 2017-01-04
- Yahoo group, 2005 to 2016
- sequence A061119 in OEIS of n^2 + 2^n
- sequence A253471 in OEIS of n^3 + 3^n
- YouTube "Leyland Numbers - Numberphile"
Number classes
| General numbers |
| Special numbers |
|
| Prime numbers |
|
