| Currently there may be errors shown on top of a page, because of a missing Wiki update (PHP version and extension DPL3). |
| Topics | Help • Register • News • History • How to • Sequences statistics • Template prototypes |
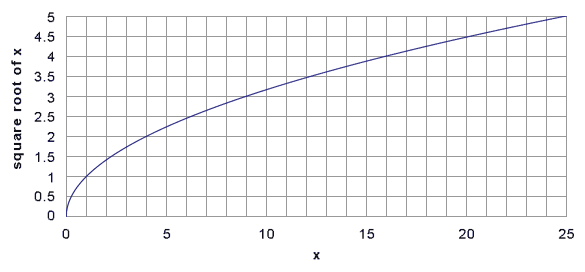
Square root
In mathematics, the principal square root of a non-negative real number
For example,
This example suggests how square roots can arise when solving quadratic equations such as
There are two solutions to the square root of a non-zero number. For a positive real number, the two square roots are the principle square root and the negative square root. For negative real numbers, the concept of imaginary and complex numbers has been developed to provide a mathematical framework to deal with the results.
Square roots of positive integers are often irrational numbers, i.e., numbers not expressible as a quotient of two integers. For example,
The discovery that
The square root symbol (√) was first used during the 16th century. It has been suggested that it originated as an altered form of lowercase r, representing the Latin radix (meaning "root").
Contents
[hide]Properties
- The principal square root function
- The principal square root function
- There are only two solutions to the equation
- To obtain both roots of a positive number, take the value given by the principal square root function as the first root (
- The following important properties of the square root functions are valid for all positive real numbers
- The square root function generally maps rational numbers to algebraic numbers;
- In geometrical terms, the square root function maps the area of a square to its side length.
- The function
- Suppose that
- In calculus, for instance when proving that the square root function is continuous or differentiable or when computing certain limits, the following identity often comes handy:
- It is valid for all non-negative numbers
- The function is continuous for all non-negative
- Its Taylor series about
- for
Computing square roots
Calculators
Pocket calculators typically implement good routines to compute the exponential function and the natural logarithm, and then compute the square root of
The same identity is exploited when computing square roots with logarithm tables or slide rules.
An exact "long-division like" algorithm
This method, while much slower than the Babylonian method, has the advantage that it is exact: if the given number has a square root whose decimal representation terminates, then the algorithm terminates and produces the correct square root after finitely many steps. It can thus be used to check whether a given integer is a square number.
Write the number in decimal and divide it into pairs of digits starting from the decimal point. The numbers are laid out similar to the long division algorithm and the final square root will appear above the original number.
For each iteration:
- Bring down the most significant pair of digits not yet used and append them to any remainder. This is the current value referred to in steps 2 and 3.
- If
- Subtract
- If the remainder is zero and there are no more digits to bring down the algorithm has terminated. Otherwise continue with step 1.
Example: What is the square root of 152.2756?
1 2. 3 4
| 01 52.27 56 1 The digit 1 is a solution digit
x 01 1(20*0+1)=1 +1
00 52 22 The digit 2 is a solution digit
2x 00 44 2(20*1+2)=44 + 2
08 27 243 The digit 3 is a solution digit
24x 07 29 3(20*12+3)=729 + 3
98 56 2464 The digit 4 is a solution digit
246x 98 56 4(20*123+4)=9856 4
00 00 Algorithm terminates: answer is 12.34
Although demonstrated here for base 10 numbers, the procedure works for any base, including base 2. In the description above, 20 means double the number base used, in the case of binary this would really be 100. The algorithm is in fact much easier to perform in base 2, as in every step only the two digits 0 and 1 have to be tested.
Bakhshali approximation
The Bakhshali square root approximation is a mathematical method for finding an approximation to a square root which was described in an ancient manuscript by the name of "The Bakhshali Manuscript" because it was discovered in 1881 near the village of Bakhshali (or Bakhshalai) in the Yusufzai subdivision of the Peshawar district (now part of Pakistan). The manuscript was made out of the leaves of birch bark tree and was written in Sarada script.
The Bakhshali square root approximation is just the simple approximation applied twice.
- Let
- Let
When expanded, the equation becomes
Bakhshali approximation example
Find
- Using
Simple approximation
The simple approximation is rather simple and can be highly inaccurate. The amount of inaccuracy for this approximation is dependent on the value of the expression
Construction
If N > 0 and d > 0 then
So the solution for
Thus
Babylonian method
A commonly used algorithm for approximating
- start with an arbitrary positive start value
- replace
- go to 2
This is a quadratically convergent algorithm, which means that the number of correct digits of
This could be represented as
where
This algorithm works equally well in the p-adic numbers, but cannot be used to identify real square roots with p-adic square roots; it is easy, for example, to construct a sequence of rational numbers by this method which converges to
Square roots of the first 20 positive integers
External links
- Japanese soroban techniques - Professor Fukutaro Kato's method
- Japanese soroban techniques - Takashi Kojima's method
- Algorithms, implementations, and more - Paul Hsieh's square roots webpage
- Wikipedia